Bài 4: NHIỆT DUNG RIÊNG
👀 66
❤️ 1
Cập nhật gần nhất: 5 months ago
I. KHÁI NIỆM NHIỆT DUNG RIÊNG
1. Hệ thức tính nhiệt lượng:
Trong đời sống, khi muốn làm nóng hoặc làm lạnh một vật, chúng ta phải cung cấp hoặc lấy đi một lượng nhiệt. Lượng nhiệt này phụ thuộc vào ba yếu tố chính:
Khối lượng của vật – Vật có khối lượng càng lớn thì cần nhiều nhiệt hơn để thay đổi nhiệt độ.
Độ tăng (hoặc giảm) nhiệt độ của vật – Muốn thay đổi nhiệt độ càng nhiều thì cần truyền nhiệt càng nhiều.
Tính chất của chất làm vật – Mỗi chất khác nhau sẽ cần lượng nhiệt khác nhau để thay đổi cùng một mức nhiệt độ.
Thí nghiệm cho thấy:
Nhiệt lượng Q cần truyền cho vật tỉ lệ thuận với khối lượng m của vật.
Nhiệt lượng Q cũng tỉ lệ thuận với độ tăng nhiệt độ ΔT của vật.
Vì vậy, ta có:
\(\frac{Q}{m \Delta T} = hằng số \)
Hằng số này đặc trưng cho từng chất và được gọi là nhiệt dung riêng của chất, ký hiệu là c.
Công thức tính nhiệt dung riêng:
\( c = \frac{Q}{m \Delta T}\)
Đơn vị: J/(kg.K)
Từ đó, công thức tính nhiệt lượng khi làm thay đổi nhiệt độ của vật là:
Q = mcΔT
Trong đó:
m: khối lượng của vật (kg).
c: nhiệt dung riêng của chất làm vật.
ΔT: độ tăng hoặc giảm nhiệt độ (K hoặc °C)
2. Định nghĩa nhiệt dung riêng:
Từ công thức tính nhiệt dung riêng:
\( c = \frac{Q}{m \Delta T}\)
Ta có thể rút ra định nghĩa về nhiệt dung riêng của một chất:
Nhiệt dung riêng( kí hiệu c) của một chất là nhiệt lượng cần thiết cung cấp cho 1kg chất đó tăng 1K.
3. Một số dạng toán
a. \(Q_{tỏa} = Q_{thu}\)
Áp dụng định luật bảo toàn năng lượng thì một vật nóng tiếp xúc vật lạnh. Nhiệt lượng vật nóng tỏa ra bằng nhiệt lượng vật lạnh thu vào
Ví dụ: cho 1kg nước nóng ở 80°C vào 2kg nước lạnh ở 20°C. Tính nhiệt độ cân bằng. Nhiệt dung riêng của nước là 4200J/Kg.K.
Giải:
Áp dụng định luật bảo toàn năng lượng ta có:
\(Q_{tỏa} = Q_{thu}\)
Tương ứng:
\(1 . 4200 . (80 - t_{cb}) = 2 . 4200 . (t_{cb}-20)\)
Giải phương trình 1 ẩn ta được:
\(t_{cb} = 40°C\)
Đáp số: 40°C
b. Công suất và hiệu suất bếp
Công suất (P)
Công suất là công (hoặc công suất nhiệt) thực hiện trên một đơn vị thời gian.
Công thức:
\( P = \frac{ Q}{t}\)
Trong đó:
P : công suất (W)
Q : nhiệt lượng cung cấp (J)
t : thời gian (s)
Đơn vị W (Watt): 1 W=1 J/s.
Trong thực tế: bếp điện thường có công suất đặt (ví dụ 2000 W = 2,0 kW).
Hiệu suất (H)
Hiệu suất của bếp là tỉ số giữa nhiệt lượng hữu ích dùng để làm nhiệm vụ (ví dụ làm nóng nước) và năng lượng đầu vào (điện năng hoặc năng lượng do nhiên liệu cung cấp):
\( H = \frac{Q_{hữu ích}}{E_{đầu vào}}\)
Nếu tính theo công suất và thời gian:
\( H = \frac{Q_{hữu ích}}{Pt}\)
Hiệu suất thường < 1 (thường tính theo %)
Nguyên nhân thất thoát: thất thoát ra không khí, làm nóng dụng cụ, bức xạ, dẫn nhiệt ra môi trường,…
Ví dụ 1 — Bếp điện (tính thời gian, tính hiệu suất)
Bài toán: Dùng bếp điện có công suất định mức P = 2,5 kW để đun 2 kg nước từ 20°C đến 100°C. Biết nhiệt dung riêng của nước 4200 J/Kg.K. Bỏ qua tổn thất (giả sử hiệu suất = 100%).
Tính: (a) Nhiệt lượng cần (b) Thời gian cần.
Lời giải:
(a) Nhiệt lượng cần:
Q = mcΔT = 2 . 4200 . (100−20)
Q= 2 . 4200 . 80 = 672000 J.
(b) Thời gian (với P=2500 W)
\( t = \frac{Q}{P} \)
\( t = \frac{672000}{2500} ≈ 268,8 s ≈ 4,48 phút \)
Nếu hiệu suất thực tế chỉ là 80% (H = 0,8), năng lượng cần cung cấp là
\( Q_{bếp} = \frac{Q_{nước nhận}}{H} \)
\( Q_{bếp} = \frac{672000}{0,8} = 840000J \)
Khi đó thời gian:
\( t = \frac{840000}{2500} ≈ 336 s≈5,6 phút \)
4. Ví dụ 2 — Bếp gas (tính hiệu suất)
Bài toán: Dùng bếp gas đun 1 kg nước từ 25°C đến 85°C cần 5 gam gas. Biết nhiệt dung riêng của nước là 4200J/Kg.K và năng suất tỏa nhiệt của gas là \(5,5.10^7 J/Kg \). Tính hiệu suất bếp.
Giải:
Nhiệt lượng cần thiết để đun nước:
\( Q_{nước nhận} = mcΔT = 1 . 4200 . (85 - 25) = 252000 J \)
Nhiệt lượng mà gas tỏa ra:
\( Q_{gas} = q. m = 5,5.10^7 . 5 . 10^{-3} = 275000 J \)
Hiệu suất bếp là:
\(H = \frac{Q_{nước nhận}}{Q_{gas}} \)
\( H = \frac{252000}{275000} = 0,916 \)
Đáp án: 91,6%
Kết luận ghi nhớ:
Nhiệt dung riêng( kí hiệu c) của một chất là nhiệt lượng cần thiết cung cấp cho 1kg chất đó tăng 1K.
Công thức tính nhiệt lượng khi làm thay đổi nhiệt độ của vật là:
Q = mcΔT
Trong đó:
m: khối lượng của vật (kg).
c: nhiệt dung riêng của chất làm vật.
ΔT: độ tăng hoặc giảm nhiệt độ (K hoặc °C)
\( P = \frac{ Q}{t}\)
\( H = \frac{Q_{hữu ích}}{E_{đầu vào}}\) trường hợp công suất \( H = \frac{Q_{hữu ích}}{Pt}\)
II. THỰC HÀNH ĐO NHIỆT DUNG RIÊNG CỦA NƯỚC
1. Mục đích
Xác định nhiệt dung riêng của nước bằng phương pháp đun nước bằng bếp điện (dùng bộ đun điện có công suất xác định).
Luyện kỹ năng đo, ghi và xử lý số liệu: lập bảng, vẽ đồ thị t theo τ, tính trung bình và ước lượng sai số.
2. Dụng cụ
- Bình nhiệt lượng kế (có lớp cách nhiệt) kèm nắp có gắn điện trở đốt.
- Nguồn điện 1 chiều hoặc bộ nguồn có đồng hồ đo công suất (hoặc dùng Vôn kế và ampe kế để xác định công suất P = U.I) để xác định công suất điện P của điện trở.
- Nhiệt kế điện tử (hoặc cặp nhiệt điện) độ phân giải ≈ 0,1°C.
- Cân điện tử (đo khối lượng nước).
- Cốc đong, thìa khuấy, dây nối, đồng hồ bấm giây.
- Ghi chú: cách nhiệt tốt giúp giảm sai số do truyền nhiệt ra môi trường.
3. Lý thuyết và công thức chính
Nhiệt lượng cần truyền để làm tăng nhiệt độ một khối chất:
Q = mcΔt
với m (kg), c (J·kg⁻¹·K⁻¹), Δt (K hay °C).
Khi dùng bộ đun điện có công suất P chạy trong thời gian Δτ, năng lượng điện phát ra:
Q = PΔτ.
Giả sử tất cả năng lượng điện truyền vào nước (và phần lớn vào mẫu), ta có:
PΔτ = mcΔt
Trong thực nghiệm biểu diễn t theo τ (điểm nhiệt độ theo thời gian) ta thường chọn hai điểm \(M(t_M, τ_M) \text{và} N(t_N, τ_N)\) nằm trên đoạn tuyến tính tránh vùng đầu (trục số ban đầu có dao động). Khi đó:
\( c = \frac{P(τ_N - τ_M)}{m(t_N - t_N)}\)
4. Thiết kế phương án thí nghiệm (các bước chi tiết)
Chuẩn bị:
Cân lượng nước cần dùng → ghi m (kg). Đổ nước vào bình nhiệt lượng kế.
Đặt nhiệt kế trong nước (không chạm đáy), lắp hoàn chỉnh hệ thống đun.
Xác định công suất điện P của nguồn/điện trở (có thể dùng Vôn kế cùng ampe kế rồi áp dung P = U . I hoặc đọc công suất trên bộ đo công suất). Ghi P (W).
Tiến hành đo:
- Ghi lại nhiệt độ ban đầu τ = 0
- Bật nguồn, bắt đầu đếm thời gian τ. Khuấy nhẹ và đều trong suốt thí nghiệm để nhiệt độ trong bình đồng nhất.
- Ghi nhiệt độ t theo các thời điểm 𝜏 đều nhau (ví dụ mỗi 60 s). Ghi ít nhất 6–8 cặp (τ,t) trải đều trong khoảng tăng nhiệt.
- Tắt nguồn sau khi đủ số mẫu.

Ghi bảng dữ liệu (mẫu bên dưới).
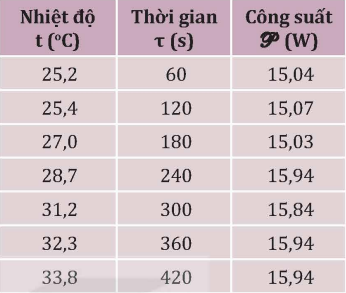
Vẽ đồ thị t theo τ. ( mẫu minh họa bên dưới)
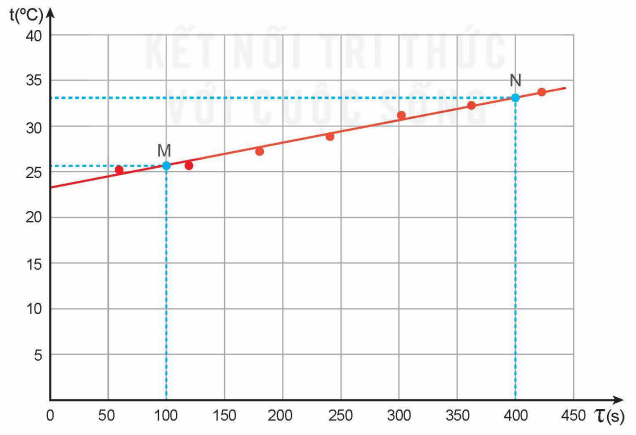
Áp dụng công thức:
\( c = \frac{P(τ_N - τ_M)}{m(t_N - t_N)}\)
Giả sử khối lượng nước
m=0,15 kg.
Chọn M: \(τ_M = 120 s, t_M = 25,4 °C\).
Chọn N: \(τ_N = 420 s, t_N = 33,8 °C\).
Công suất trung bình
\(\overline{P} ≈ 15,04 W\) (có thể lấy trung bình các P).
Δτ = 420 - 120 = 300s, Δt = 33,8 - 25,4 = 8,4°C
\( c = \frac{15,04 . 300}{1,5 . 8,4} ≈ 3581 J/Kg.K\)
Nhận xét: Kết quả thấp hơn 4200 vì có tổn thất nhiệt ra môi trường.
Bài tập ôn tập (19 tổng câu hỏi)
*Lưu ý: làm hết câu này rồi đến câu khác. Xin đừng nôn nóng.Đang tải câu hỏi...
